SAT – Math
What does the SAT Math Section test?
The Math section is designed to assess your understanding of mathematical concepts and your ability to apply them to real-world problems. The SAT Math section is divided into two parts – a calculator portion and a no calculator portion.
The SAT Math section tests a variety of mathematical skills, including algebra, geometry, trigonometry, and data analysis. You will be asked to solve problems that involve equations, graphs, and tables, and you may be required to interpret information from charts or diagrams.
The Math section includes both multiple-choice questions and grid-in questions. For multiple-choice questions, you will choose the correct answer from a set of options. For grid-in questions, you will solve the problem and then enter your answer into a grid.
For a list of permitted calculators on the calculator portion of the math test CLICK HERE.
To perform well on the SAT Math section, it’s essential to be familiar with the content and format of the exam, and to practice solving a variety of math problems.
Math (no-calculator) Examples
Example #1: Enter your response into the appropriate grid below.
Mildred’s elementary school teacher is 7 years less than the square of her age. If her teacher is 57 years old, how old is Mildred?
Answer: The only answers that work in the grid are: 8, 08, 008, 0008, 08., 008., 8., 8.0, 8.00 or 08.0. Let’s translate the above into an equation, using M for Mildred’s age and T for her teacher’s age. T = M2-7. We are told that T = 57, so plugging in the value of T, we have 57 = M2-7. Add 7 to both sides of the equation to get 64 = M2. Now taking the square root of each side, we get M = 8. Mildred is 8 years old.
Example #2
If today is Wednesday, what day of the week was it 71 days ago?
- Tuesday
- Wednesday
- Thursday
- Friday
Answer: A – Let’s divide by 71 and see what the remainder is: 71/7=10 with a remainder of 1. We know that 70 days ago, it was a Wednesday (because 70/7=10 and 10 weeks ago, it was the same day of the week as today). We have to go back 1 more day, however. The day before Wednesday is Tuesday, so 70+1=71 days ago, it was a Tuesday. The correct answer is A. Tuesday.
Example #3
Given: 6a – b2=11c. If b + a = 7, then what is abc, if a, b, and c are all positive integers?
- 11
- 10
- 9
- 8
Answer: B – The best way to solve this problem is to start making assumptions and then plugging in values for a and seeing if we can find values for b and c that make sense. If 6a – b2 = 11c, then let’s assume c = 1. If c is a higher number, this equation gets way too complicated to solve, so this is a fair assumption to begin with. If c = 1, then let’s see if a = 1 also works. If so, 61 – b2 = 111 → b2 = 6 – 11 = -5. b2 ≠ -5 does not make sense, so a ≠ 1. Now let’s try a = 2:62 – b2 = 111 → b2 = 62 – 111 = 36 – 11 = 25. Can b2 = 25? Yes. If b = 5, then this equation makes sense. So, our initial assumption about c = 1 was correct, and a = 2, b = 5 and c= 1. The question asks for abc=2 x 5 x 1 = 10. The correct answer is B. 10.
Example #4
The diagram below is formed using 8 symmetric triangles. What is the ratio of the shaded area to the area of the rectangle?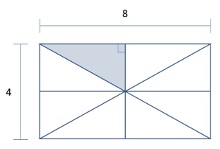
- 1:2
- 1:4
- 1:6
- 1:8
Answer: D – The area of the large outer rectangle is length x width = 8 x 4 = 32. The formula for the area of a triangle is (base x height)/2. Whether we use 4 ÷ 2 as the base and 8 ÷ 2 as the height or 8 ÷ 2 as the base and 4 ÷ 2 as the height does not matter, as they lead us to the same answer. (4 x 2)/2 = 4. The ratio of the shaded area to the outer rectangle is 4:32 or 1:8. The correct answer is D. 1:8.
Math (calculator) Examples
Example #1
A rectangle intersects a circle, as shown in the figure below. If the radius of the circle is equal to both half the length of the rectangle and to the width of the rectangle, what is the area of the shaded region?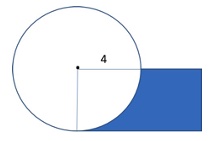
- 3.43
- 18.27
- 19.43
- 28.86
Answers: C – The area of the shaded region is the area of the rectangle minus one-fourth of the area of the circle. If r = 4, that means the width of the rectangle is also 4 and the length is 2 x 4 = 8 units. The area of the rectangle is 8 x 4 = 32 units2 and the area of the circle is ℼr2 =ℼ(4)2 = 16ℼ. One-fourth of this is: ¼ x 16ℼ = 4ℼ or 12.57. The area of the shaded region is 32 – 4ℼ or 32 – 12.57 = 19.43. The correct answer is C. 19.43.
Example #2
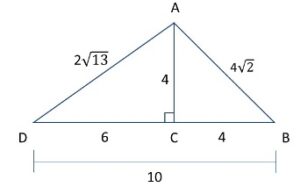
What is the length of AD + AB in the figure below if AC = 4, DB =10 and Triangle ACB is an isosceles triangle?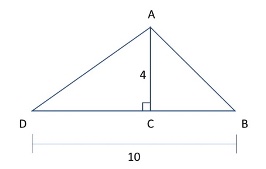
- 12.73
- 24.04
- 14.28
- 12.87
Answers: D – We are told that Triangle ACB is an isosceles triangle. If AC = 4, then CB = 4 as well. Using the Pythagorean Theorem, we can find AB: 42 + 42 = AB2 → 32 = AB2 and AB = 4√2 or 5.66. Next, we are given that DB = 10. Since we found that CB = 4, DC must be 10 – 4 = 6. We can use the Pythagorean Theorem to find the hypotenuse of Triangle ACD: 42 + 62 = AD2 → 16 + 36 = 52 = AD2. Taking the square root of each side, we get AD = 2√13 or 7.21. The question asks for AD + AB = 5.66 + 7.21 = 12.87. The correct answer is D. 12.87.
Example #3
In the diagram below, we are given two sets of parallel lines intersected by a third line AB. What is the value of x + y + z?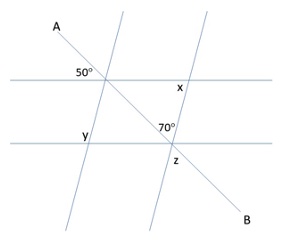
- 260º
- 250º
- 240º
- 230º
Answers: B – To make this question easier to explain, we can attach letters to every angle, to better explain which angles are equal. We are given that h = 50°, therefore e = 50° as well since they are opposite angles. Learning the value of e helps us to calculate x, since e+x+s=180°. So, x = 180 – 50 – 70 = 60°. If x = 60°, then i = 60° as well since they are also opposite angles. t=60° as well since i and t are corresponding angles. We also know that since s = 70°, z = 70° as well since they too are opposite angles. We now only need to solve for y to be able to calculate x + y + z. We already calculated that i = 60°, so k = 180 – 60 = 120° since i and k are supplementary angles (which must add up to 180°). We can now find that y = k = 120° since y and k are corresponding angles. x + y + z = 60 + 120 + 70 = 250°. The correct answer is B. 250°.
Example #4
At a NYC public beach, lifeguards are paid differently depending on their previous experience. The 8 lifeguards on the payroll get paid according to the chart below:
| # of Lifeguards | Pay Per Hour |
|---|---|
| 1 | $10 |
| 1 | $11 |
| 3 | $12 |
| 2 | $15 |
| 1 | $17 |
What is the mean hourly pay for the lifeguards?
- $12
- $13
- $14
- $15
Answers: B – The mean is the average. Here, there are a total of 8 lifeguards, so we should set up the formula to be: ($10+$11+$12+$12+$12+$15+$15+$17)/8 = $104/8 = $13. The correct answer is B. $13.
See if TestingMom.com supports your child’s test by your school district. If you don't see your child's school district listed, check with us! We have practice for other tests as well.



Tell us about your experiences